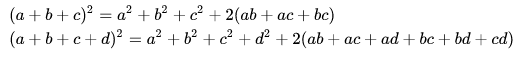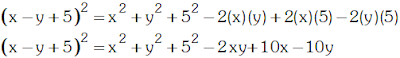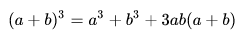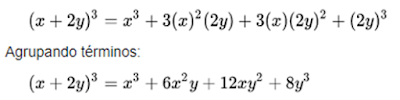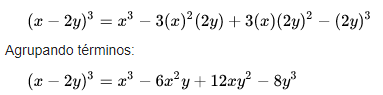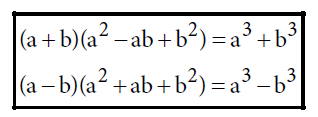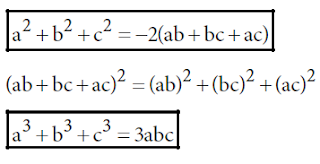Los trinomios en los productos notables

 

    LOS PRODUCTOS NOTABLES II 👀

    Con posterioridad a Al - Khuwarizmi se desarrollaron una infinidad de procedimientos de cálculo y algoritmos especiales, entre ellos: la Obtención del número pi con 17 cifras exactas mediante polígonos inscritos y circunscritos en la circunferencia realizada por Kashi (s. XV). 

    Después de más de 150 años, en 1593, en Europa, Viète encontró sólo nueve cifras exactas. Hubo que esperar a fines del siglo XVI y comienzos del XVII para repetir el cálculo de Kashi. cálculo de raíces por el método conocido actualmente como de Ruffini - Horner, posiblemente como resultado de la estrecha colaboración con los matemáticos chinos. Además fue advertida y expresada la serie del desarrollo binomial y fue también enunciada la tabla de coeficientes binomiales. Extracción aproximada de raíces, utilizando la interpolación lineal.

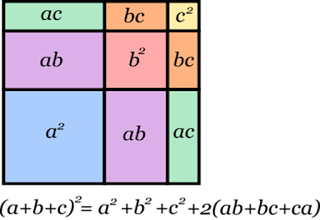
¿Qué es el cuadrado de un trinomio?

    Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos. Así considerando las variables "a", "b" y "c", se generan las siguientes formulas:

    Para su demostración, enfoquémonos en lo siguiente:

La suma de las áreas parciales es igual al área total, veamos:

    Sencillo, si consideramos a cada bloque como parte de la formula, ahora veamos un par de ejemplos desarrollados:

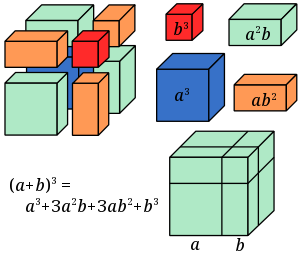
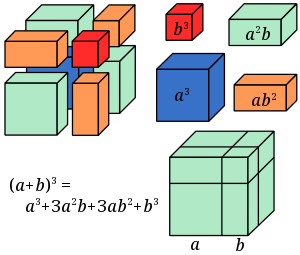
Cubo de un binomio 

Para calcular el cubo de un binomio se suman, sucesivamente:

• El cubo del primer término.
• El triple del producto del cuadrado del primero por el segundo.
• El triple del producto del primero por el cuadrado del segundo.
• El cubo del segundo término.

 Para su demostración, enfoquémonos en lo siguiente:

La suma de volúmenes parciales es igual al volumen total, veamos: 

    En el álgebra lineal, la fórmula de Cauchy–Binet, se emplea como una identidad para el determinante del producto de dos matrices rectangulares de formas transpuestas (de modo que el producto sea cuadrado y bien definido). Aquí como parte de los Productos notables, esta seria su identidad:

    Apliquemos esto en un ejemplo:

Si la operación del binomio implica resta, el resultado es:

• El cubo del primer término.
• Menos el triple del producto del cuadrado del primero por el segundo.
• Más el triple del producto del primero por el cuadrado del segundo.
• Menos el cubo del segundo término.

    Apliquemos esto en un ejemplo:

Suma y diferencia de cubos:

Identidades condicionales:

Si:  a + b + c = 0; se verifican:

REFERENCIAS:

- Matemáticas. Postigo L. España 1983

- Álgebra, teoría y problemas, tomo I, 2Ed. Quijano J. Perú 1995

- Algebra. LEXUS. Perú 2006.